单变量线性回归
Linner Regression with One Variable
单变量线性回归用于预测单个输入变量x与他的输出y的一种对应方式。
模型表示
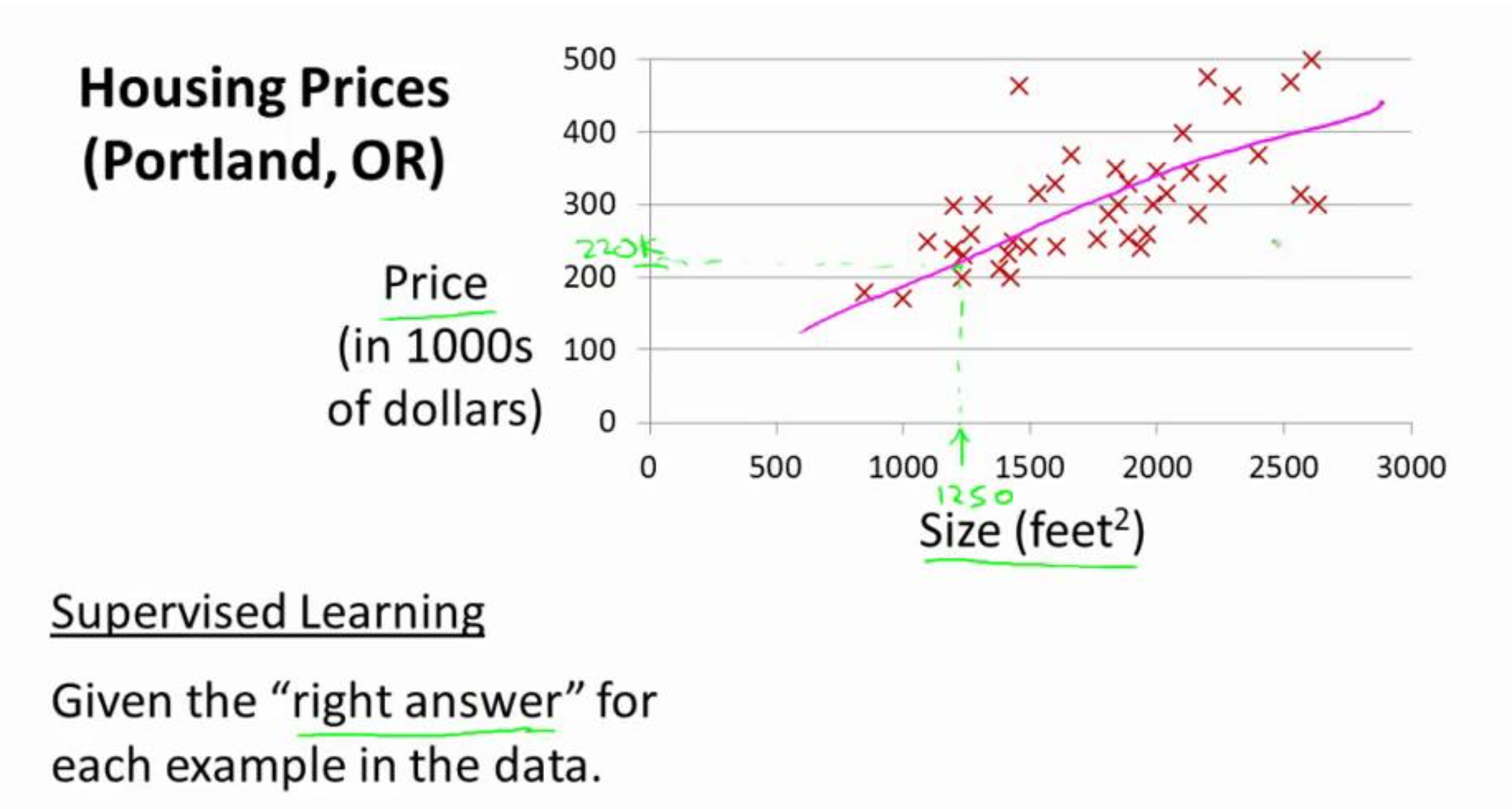
上图展示了一个单变量线性回归模型的构造思路。
首先,图上的红x为每个输入的数据set,根据数据的分布方式,大概可以用一条线(图上红色的直线)来拟合,这样。我们就能够使用公式来表示数据输入的规律。
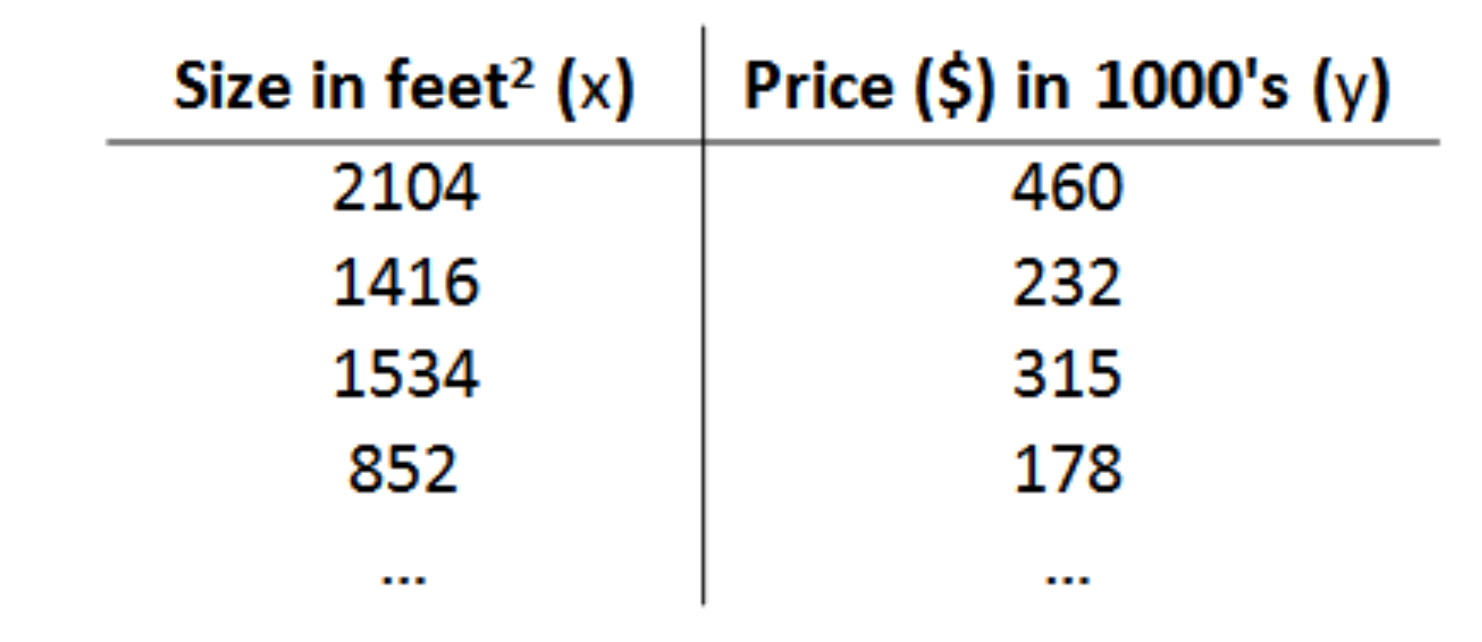
这张图上每一行为一个数据单元。左列为数据的输入x(房屋尺寸),右列为输出数据y(房屋的售出价格)。
这样。每一个数据单元就代表了一个第一张图中的一个红x。
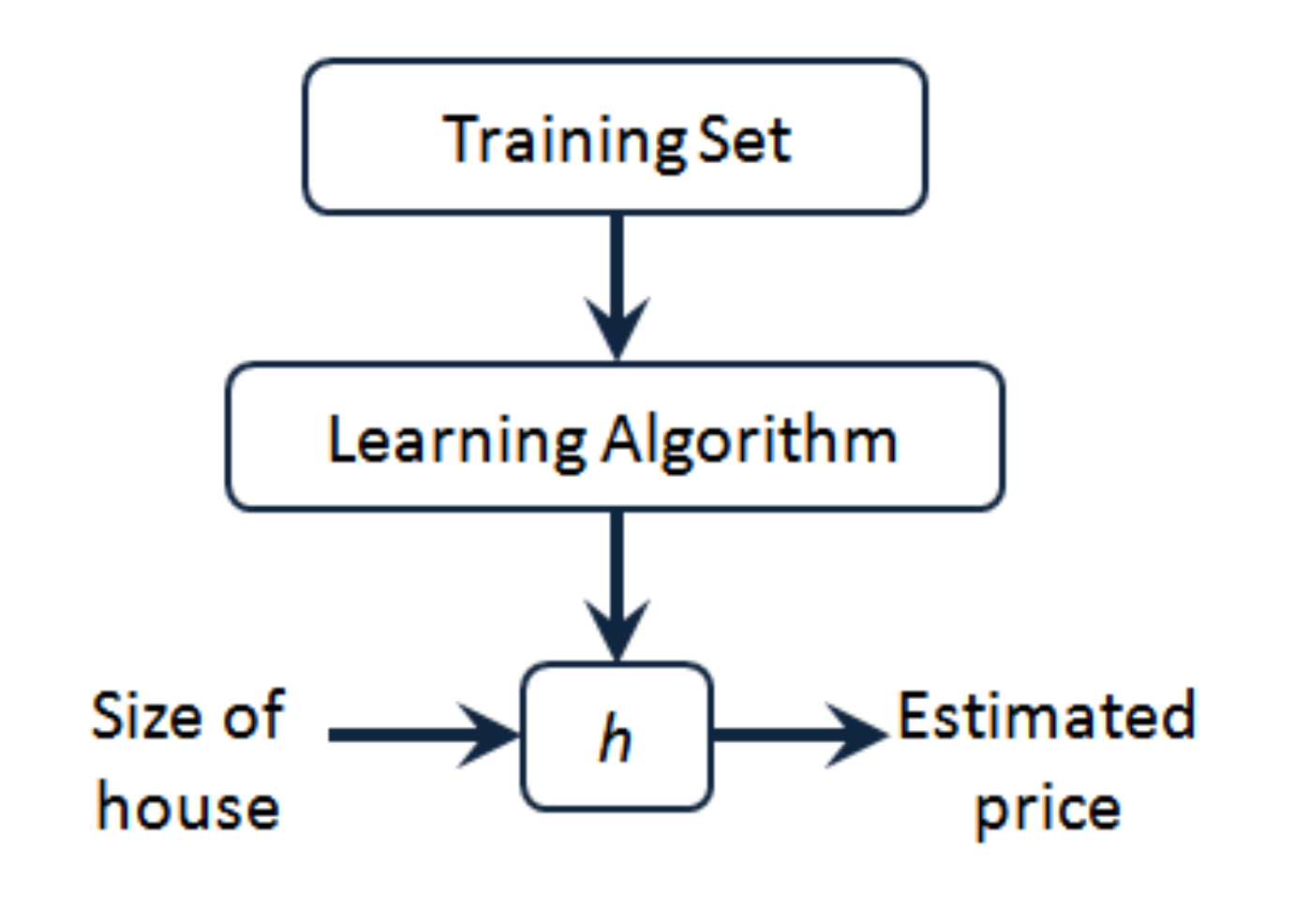
这是一个模型生成的过程,
Training set中。我们准备训练的数据。(本节中为单属性数据)。
Learning Algorithm 这里就是我们将要设计的学习算法。将ts中的数据作为输入,用来预算出最后的h。
h为我们期望的公式hypothesis ,本节中为
$$
h\theta(x)=\theta0+\theta_1
$$
代价函数
首先我们先看看代价函数的模样
$$
J(\theta_0,\theta1)=\frac1{2m}\sum{i=1}^m(h_\theta(x^{(i)})-y^{(i)}))^2
$$
J代表代价函数,这里的代价函数之时针对于线性回归函数的一个比较好的解。
后面的h代表上一节中hypothesis得到的函数带入x^i后与原始的x对应y点的差
为何需要代价函数?
上一节中。我们获得了h,但是我们没有一个方法能够正确的求解出theta的值,那么,这时我们就需要曲线救国,用代价函数来替代h,从下图看。我们只需要求出使得j最小的点的值就能很好的表示我们数据。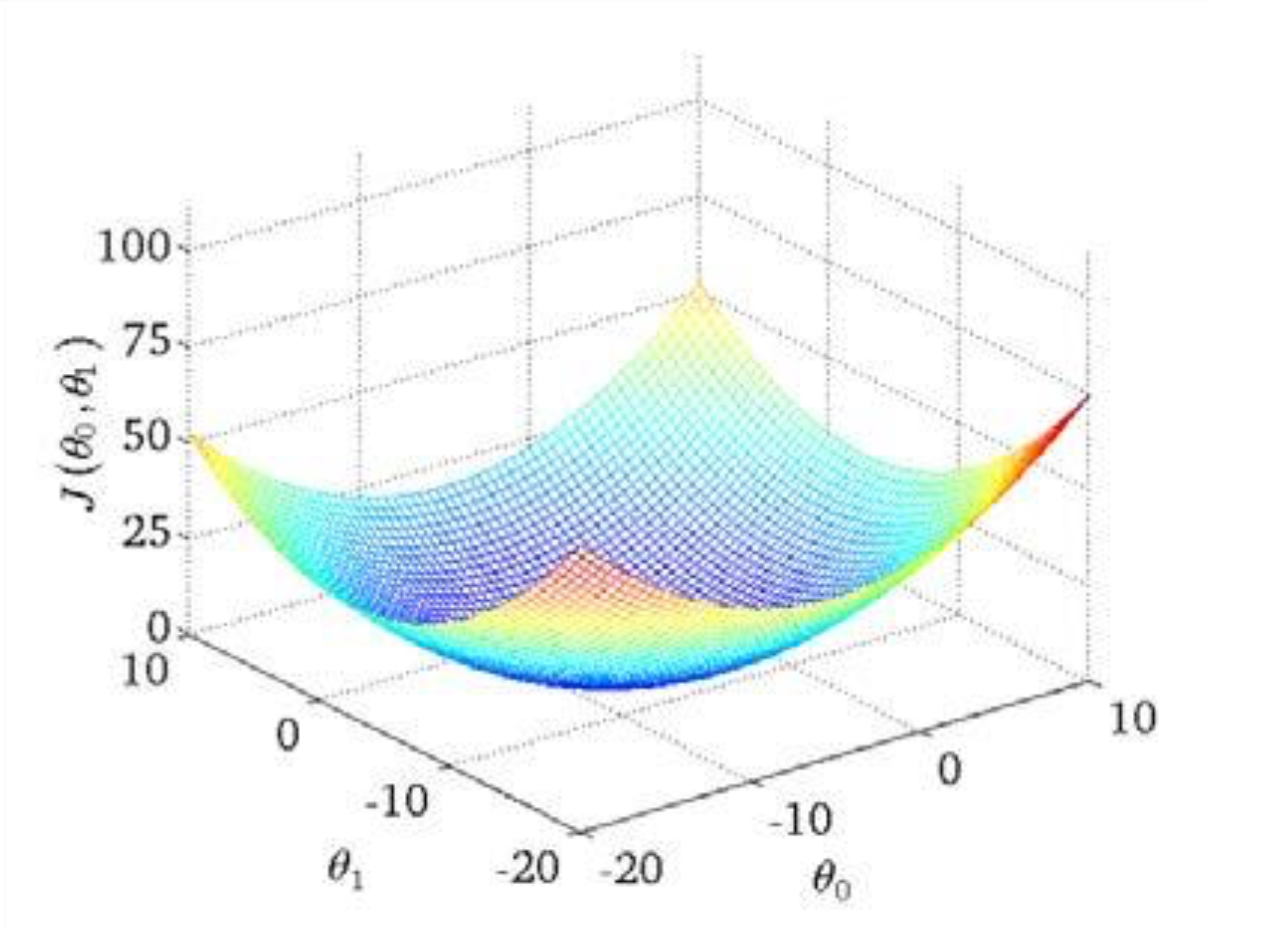
梯度下降
梯度下降是一个用来求最小值的方法,我们用梯度下降来求j的最小值
$$
\theta_j:=\theta_j-\alpha\frac{d}{d\theta_j}J(\theta)
$$
导数的作用为求出J函数所在theta点的斜率,那么,当斜率为0的时候我们就能够得到最小的值。
\alpha为学习率。如果a太小,那么我们要经过很多步的运算才能得到最小值,如果a太大,会跳过最小值,使得函数无法收敛。
在上代价函数中,我们有两个theta,那么每次变化theta的值我们都要经过这样一个过程:

temp0为我们改变theta0的值,temp1为改变theta1后的值。最后两个一起改变。
梯度下降的线性回归

这是之前的梯度下降和线性回归的算法,结合之后为下图。
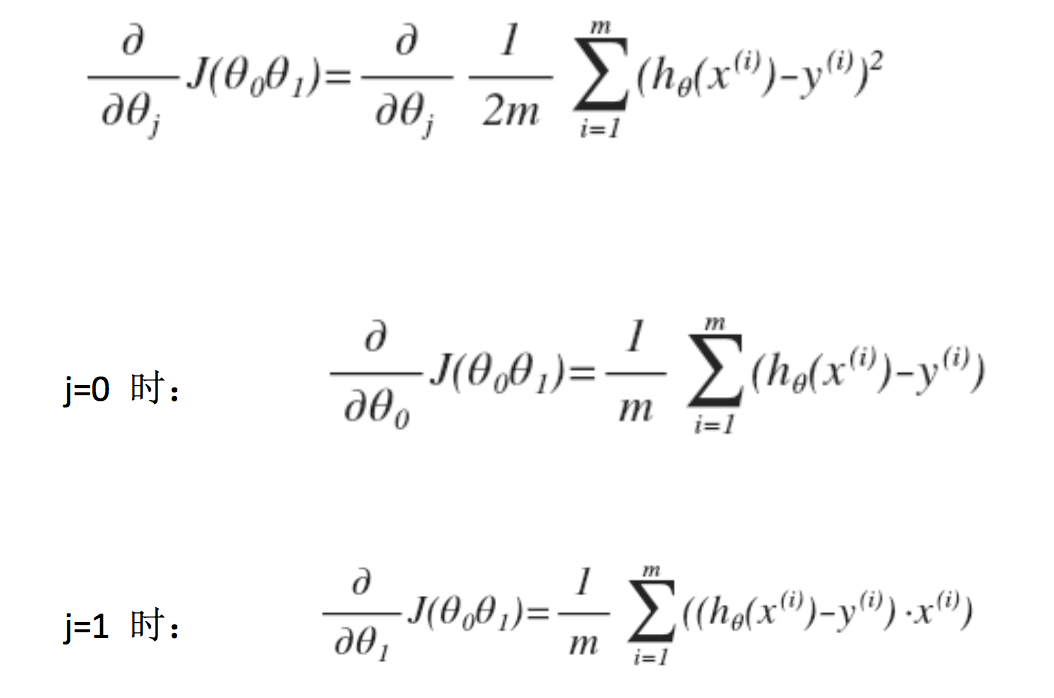
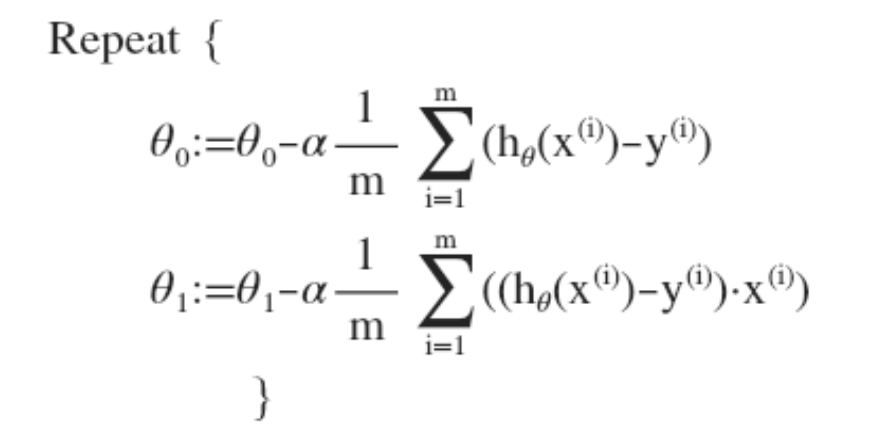
最终我们得到这样的一个求值等式。